Een geodetische koepel is een bolvormige structuur, 'geodetische' betekenis aarde te delen in het Latijn. De contouren van zelfdragende driehoeken worden geëxploiteerd in een geodetische model om de hoogste structurele voordeel te geven, dus theoretisch maakt minimaal gebruik van middelen. Het brengt de energie-efficiëntie (maximaal volume bedekt met minimale oppervlakte en een betere natuurlijke stroming van lucht) van een bolvormig gebaseerde structuur en heeft ook een betere structurele betrouwbaarheid en flexibiliteit dan rechtlijnige vormen. De gebogen vorm van deze structuur versterkt de betrouwbaarheid door het creëren van een lichte vorm die kan doorstaan en bestand tegen veel kracht dan andere modellen. Hieronder is een stap voor stap handleiding om uw eigen geodetische model te maken met schaalbare plannen.
Stap 1
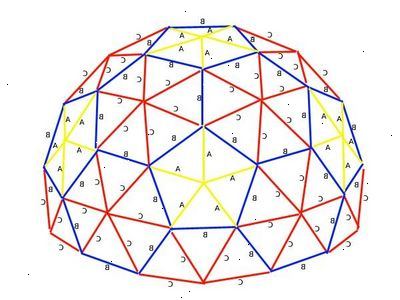
Definitie. Een geodetische koepel is opgebouwd door de vaststelling van samen een volledige rooster van driehoeken. Dit helpt om een zelfdragende structuur die op zichzelf te maken, zonder buiten fundering of basis, gebruikmakend van de minimale hoeveelheid materiaal die vlot beschikbaar en overvloedig. Een geodetische is gedefinieerd als de kortste afstand tussen twee punten op een bol of soortgelijke structuren.
Stap 2
Geschiedenis. Dit idee werd voor het eerst gepostuleerd door een Duitse ingenieur - Dr Walther Bauersfeld. Hij wordt gecrediteerd met de bouw van 's werelds eerste projectie planetarium, een structuur gevestigd op Jena, Duitsland, de weg terug in 1922. Het krediet voor het gebruik van de geodetische koepel concept voor huisvesting gebruikte gaat naar Buckminster Fuller, die zijn eerste patent geregistreerd in 1954.
Stap 3
Het maken van de driehoeken. Maak twee driehoeken van zowel dikker papier of transparanten van de volgende metingen (die de relatie tussen de zijden essentieel):
Ingesteld | Kant A | Kant B | Side C |
Side Combinatie | Aantal driehoeken (panelen) |
| Set1 | 0.3486 | 0.4035 | 2AB | 30 | |
| SET2 | 0.4035 | 0.4124 | 2CB | 75 |
Voeg een opvouwbare flap op de rand te vergemakkelijken verbinden van de driehoeken met lijm
Join kant C van zes Set 2 panelen aan een zeshoek (zes-zijdige figuur) maken met de buitenste zijden alle Side B. 10 dergelijke zeshoeken van 6 Set 2 panelen Bouwen met elk zeskant het maken van zeer lage koepels.
Doe vier driehoeken van Side C met 3 Kant B hoekpunten raken vijf ½ zeshoeken te maken.
Doe Kant A van 5 Set 1 panelen tot een vijfhoek te creëren (vijf-zijdige figuur) met Kant B het maken van de omtrek. Maak 6 dergelijke vijfhoeken. We maken de koepel van boven naar beneden met een Set 2 vijfhoeken het maken van de top.
Geregistreerd 5 zeshoeken met een pentagon aan hun kant B teneinde een minder ondiepe koepelvorm maken.
Nu de resterende driehoeken, open Kant B van de zeshoeken, verbind 5 vijfhoeken. Ga verder door toe te treden 6 zeshoeken aan de open kant B van de vijfhoeken. Nu, wat er nog zijn de 5 halve zeshoeken. Doe dit aan de open zijden van de zeshoeken en uw geodetische koepel is gedaan!
Opmerking: Het maken van dit model met stutten in plaats van panelen, zou vereisen dat u tot 30 A veerpoten, 55 B veerpoten en 80 C struts te maken met dezelfde lengte proporties. . Er dient te worden ingezet op de grond om te voorkomen dat wordt bewogen door de wind.
Terwijl de hele constructie mechanisme zou moeilijk en complex te voelen op het eerste, in werkelijkheid een geodetische koepel is een vereenvoudigde structuur, vereist weinig in termen van financiële investeringen, grondstoffen en arbeid. Het kan worden gemaakt van verschillende materialen zoals plastic, metalen golfplaten, glasvezel, enz. en gebruikt voor een veelheid van doeleinden - goedkope woningen in arme gemeenschappen, onderdak wetenschappelijke uitrusting in ongunstige klimaten, zoals de poolgebieden (Arctische en Antarctica), mobiele kampen voor militaire troepen, enz.
